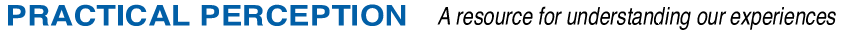Details

Last Updated: Thursday, 12 November 2015 01:35

Written by Dr. Donald H. Mershon

ADVANCED  DOWNLOAD the PDF

Summary: As discussed in the article on Basic information for depth, many different kinds of information (or cues) contribute to structuring the perceived three-dimensional environment. Not all information, however, is equally important. Gogel's Adjacency Principle states that the strength of any given cue between objects (e.g., the relative depth cue between a larger and a smaller rectangle) is an inverse function of their separation. For example, the closer the visual separation of objects in a visual display, the more effective are the cues between them in determining their relative locations in depth.  

Other articles have described (and/or elaborated upon) the various cues that we use for perceiving depth (see Basic Information for Depth and Do Smaller Things Appear Farther Away?). Another article (The Equidistance Tendency) discusses predictions for how we will perceive a depth interval when there is little in the way of available information. Specifically, the Equidistance Tendency (ET) states that we tend to see objects as if they were at the same distance, with this tendency being a stronger influence as the actual information decreases, i.e., the fewer the available cues, the greater the effect of the ET.

A "Weighting Factor"

The present article covers a different kind of influence, known as a weighting factor. Unlike the Equidistance Tendency (above), the weighting factor, known as the Adjacency Principle, does not specify that an object will tend to appear at any particular distance, but rather how different information about a given object will contribute to the way in which it's perceived. It states that the strength of any cue between objects will be inversely related to the separation of those objects. To specify the Principle in reverse, the effectiveness of a depth cue is directly related to the adjacency of the objects in question.

For the present article, we may assume that separation corresponds to the difference between the directional positions of the objects, in units of angular separation, such as degrees, minutes, radians, etc. A different article will address whether separation may also include the dimension of depth itself, as well as whether perceived separation should replace physical measures of angular separation.

Before proceeding, it is important to note that the modern development of the Adjacency Principle was the work of Walter C. Gogel, although earlier research provided background findings prior the initial publications by Gogel. The term "Adjacency Principle" itself was coined by Gogel and many papers have been published by later researchers, such as Mershon, under this label.

An Example of the Adjacency Principle in action

Consider a simple visual display that consists of two identical rectangular objects (of the same physical size and having the same h x w aspect ratio). These are positioned in front of an observer, at eye level and are observed binocularly. They are self-illuminated, being visible in an otherwise completely dark surround. The lefthand rectangle, however, is located 10 feet from the observer and the righthand one at 15 feet. Figure 1A shows a top-view of the objects in the display.

For the arrangement in Figure 1A, the cues of relative size and of stereopsis (binocular disparity) would usually provide sufficient information to allow an observer with normal vision to see that the rectangles are at different distances. Figure 1B shows the frontal view of the described display, from the observer’s viewpoint, disregarding the slight sideways shift in the images' separation (for one eye versus the other) that would create the stereoscopic cue. The blue surround in this figure (as always) indicates the fully darkened visual environment.

Figure 1
A simple visual display of two rectangular objects, one at a
distance of 10 feet and the other at a distance of 15 feet.
Only the two objects are visible, in a completely dark surround.
Image by author.

The question one might ask is this: How much depth does the observer perceive between the rectangles? Two obvious cues exist. One is based upon the disparity cue; the other is based upon the relative size cue. Fortunately for our "simple" example, both of these cues (as well as some weaker oculomotor cues) point toward the same outcome. The righthand rectangle should appear to be farther from the observer. How much farther, however, is more difficult to predict. Although the physical characteristics of the situation suggest that the "correct" answer would be that the far rectangle be seen as half again farther than the near one, this will frequently not be true.

The Adjacency Principle predicts that any/all of the cues between the rectangles should be more effective when the horizontal separation of the rectangles is less. Thus, we should expect that for the displays shown in Figure 1, decreasing the horizontal separation of the rectangles should usually create an impression of more depth and increasing the separation should create a decreased impression of depth. The change due to an increased separation (i.e., the decrease in adjacency) should continue for wider and wider gaps, until – at some point – each rectangle will appear at whatever distance it would be seen by itself – as if alone in a dark surround. The effectiveness of the relative cues to depth depends upon having the objects in a scene sufficiently close to one another.

Although the above general prediction is pretty straightforward, the exact shape of the function relating perceived depth to separation is not yet known. There are two problems. First, it is difficult to determine the separate functions for each of the cues involved. Are they all linear? Are some linear and others curvilinear? Are the slopes similar? Because virtually any display of two objects can include several depth cues, we must have some idea of how to combine these unknown functions, if we wish to make an overall prediction.

The second problem is that the Equidistance Tendency is also present and, although it is not properly called a "cue," it nevertheless has its own separation-to-strength function. Thus, it is unlikely that the overall change in apparent depth will be a single linear function, because as the separation decreases, we begin to add a tendency that counteracts the available cues. At least for very small separations, the apparent depth between our rectangles may well be less than one would expect from somewhat greater separations.

Nevertheless, despite the above limitations, there are many situations in which the Adjacency Principle provides good qualitative predictions for how cues affect apparent depth, even if such predictions are not exact. It is possible that future researchers will be able to disentangle the individual adjacency functions, and the ET function, so that more precise predictions become possible. Two further issues also complicate the picture: first, we cannot be certain that different individuals use the same cue-depth-separation functions; second, predicting the "end-point" in the apparent distances of widely-separated objects may require that we refer to other factors (see articles on the Specific Distance Tendency).

A Better Example of the Effect of Adjacency

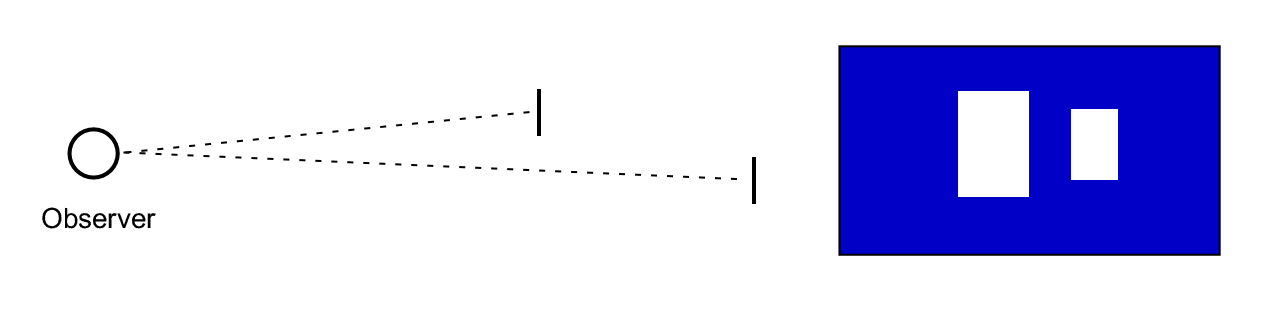
Consider the visual display shown in Figure 2. In this case, the observer is presented with two rectangles, of different size but having the same aspect ratio. The two rectangles are separated by a circular object. All three objects are actually at the same distance and all are observed monocularly.

Despite the difference in the angular sizes of the rectangles, the presence of the circular object creates a strong cue of interposition. This may be interpreted in at least two ways: 1) the interposition cue is simply a stronger factor than the relative size cue, and/or 2) the relationship that creates any interposition cue always involves very adjacent edges, giving that factor a particularly strong effect. (Note that even if the ET tends to flatten the appearance of the three objects, the relative depth ordering of the objects will remain.)

Figure 2
Three objects, observed monocularly, in an otherwise dark
surround. From left-to-right, the objects appear to be
increasingly nearer to the observer, to at least some degree.
Image by author.

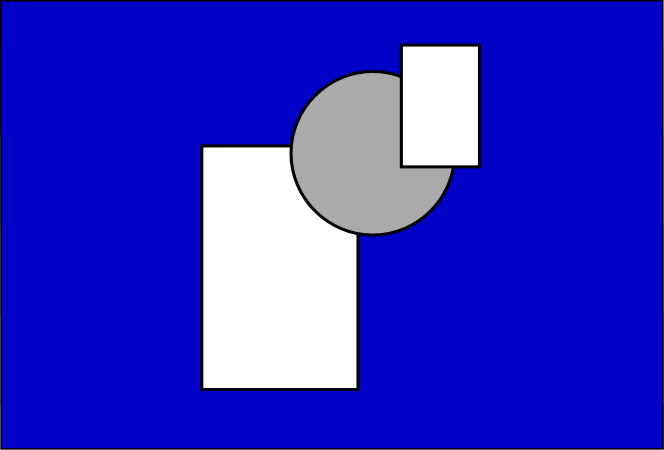
Now, we shall add two more rectangles with the same aspect ratio. Each of these matches the angular size of the previous rectangle on the right side of the original display. The new rectangles, however, are positioned as shown in Figure 3.

Figure 3
The addition of rectangles X and Y to Figure 2. As predicted from
the Adjacency Principle, the most-adjacent portions of Figure 2
dominate the perceived depth positions of X and Y.
Image by author (after Gogel, 1970).

 Although the two added rectangles might – at some level – be expected to appear at the same distance as each other, due to the zero relative size cue between them, this seldom occurs. Instead, the left-hand rectangle (X) is seen in relation to the large rectangle, appearing farther from the observer than the central display. The right-hand rectangle (Y) appears in relation to the small rectangle in the central display and their equal angular sizes result in them appearing at the same distance. Data from a variety of studies support the Adjacency Principle (see references at end of this article).

To conclude this introductory article, the Adjacency Principle has been demonstrated by the greater importance of cues between more adjacent objects. That is, X and the large rectangle involve a strong cue. Y and the small rectangle likewise involve a strong cue. The cue that might, in other circumstances, indicate that X and Y are at the same distance, is over-ridden by the cues that involve the more adjacent relationships.

Gogel, W. C.  (1965).  Size cues and the adjacency principle.  Journal of Experimental Psychology, 70, 289-293.

Gogel, W. C. (1978).  The adjacency principle in visual perception.  Scientific American, 238 (No. 5, May), 126-139.

Gogel, W. C.  (1970).  The adjacency principle and three-dimensional visual illusions. Psychonomic Monograph Supplements, 3 (No. 13), 153-169, 215-219.

Gogel, W. C., & Mershon, D. H.  (1977).  Local autonomy in visual space. Scandinavian Journal of Psychology, 18, 237–250.