Details

Last Updated: Sunday, 23 August 2015 10:56

Written by Dr. Donald H. Mershon

BASIC  DOWNLOAD the PDF

Summary: Angular measures are frequently used to describe visual stimuli. Such measures may be as simple as describing the shape of a rectangle in terms of having four right-angles. One can, however, also use angular values in a different way to describe size. It is, for example, both common and useful to measure the "retinal or angular size" of a visual stimulus in a manner that simultaneously takes into account both the physical size and the physical distance of the target.

The use of angular measures is frequently required to describe visual stimuli.  This use may be as simple as describing the angles of a square or rectangle as being right-angles or indicating the orientation of a line, with respect to the horizontal:

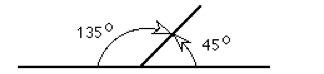
In using angular measurements, 1 degree is said to contain 60 minutes and each minute contains 60 seconds.  Another measure of angular extent is the radian, where 1 rad  =  57.29578 degrees.

One can, however, also use angular measurements in a less common manner, for describing the size of visual stimuli.  Consider the diagram below that shows an eye, two alternative objects at which the eye might look, and some lines-of-sight between the eye and the two ends of the objects.  For visual perception, the crucial stimulus is often the pattern of light as it falls on the eye. 

Although one might describe that pattern by indicating both the size and distance of the object of interest.  In many cases, however, it is more convenient to give an object's angular size (as symbolized by the Greek letter theta --- θ). This measurement is called the Visual Angle and is expressed in values such as degrees, minutes and/or seconds (see above).  Any linear dimension of a visual stimulus (height, width, etc.) may be expressed in these angular terms.  Note below that size 1 at distance 1 and size 2 at distance 2 produce equal θ.

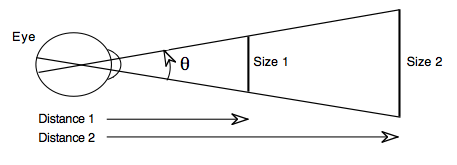
For situations in which S (size) is small, relative to D (distance), then:

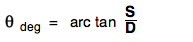
For some everyday comparisons, one can remember that, at an average arm's length of 57 cm, the horizontal width of the image of your hand is about 10 deg (10^o ) wide and that a quarter coin (2.5 cm wide) subtends a visual angle of somewhat over 2 deg (2^o ).

The quarter viewed from 82.5 m, however, subtends 1 min and, viewed from 4950 m (just over 3 miles), it subtends 1 sec.

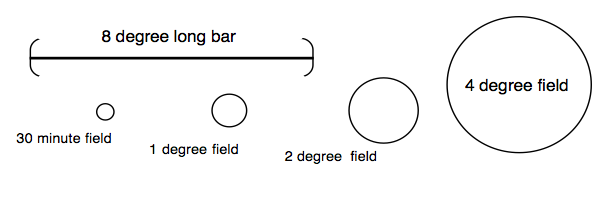
The figure below may be used to provide a rough approximation of how different angular sizes appear. Ideally, try to adjust the sizes of the targets on your display, so that each one is physically about the same length in cm as its labeled size in deg. Then position your head, so that your eyes are at what is nominally considered a reading distance (40 cm) from the display. The table below the figure will allow you to make a partial correction, if either of the above situations cannot be readily achieved.