Details

Last Updated: Sunday, 18 October 2015 23:38

Written by Dr. Donald H. Mershon

ADVANCED  DOWNLOAD the PDF

Summary: The Theory of Phenomenal Geometry (a contribution of Walter C. Gogel) provides a comprehensive description of the inter-relationships that allow us to understand the process by which we construct our internal three-dimensional world. In brief, the values of certain "primary" percepts (perceived distance, perceived direction and perceived self-movement) are determined by a variety of factors. Other, "derived" percepts (e.g., perceived size, perceived shape, perceived object motion) can be predicted from the primary percepts, by application of simple Euclidean geometry. Although the exact neural processes involved are not specified by the theory, Phenomenal Geometry encompasses an important conceptual model.  

Various articles on the Practical Perception website address issues such as the types of information (cues) used for perceiving depth and distance, as well as the manner in which some information may be weighted more strongly than other information. (The weighting issue is usually referred to as the Adjacency Principle.) Other articles have addressed how we may predict the apparent depth between objects, or predict the overall apparent distance of a given object, based upon two internal perceptual tendencies (so-called “authochthonous” factors). See articles on the Equidistance Tendency and the Specific Distance Tendency.

Although the Theory of Phenomenal Geometry is also attributable to the work of Walter C. Gogel, its contribution is quite different than the factors indicated above. The Theory provides a relatively few basic principles that can aid our understanding of how certain perceptual information may be combined to yield other percepts. And, how the knowledge of these processes can be used by anyone interested in predicting some percepts based upon others. Although this idea may sound complicated at first, the following article will lay out the fundamentals in a straightforward fashion. Later articles will elaborate.

The First Step for Understanding

There are many different kinds of perceptual variables that are involved in perceiving the spatial relationships and actions in our environment. The Theory describes three of these perceptual variables as being “primary” percepts. Many others are considered to be “derived” percepts. The connection between these two classes of perceptual variable is that the derived ones are the result of applying the laws of geometry to the primary ones.

Although mathematics includes many different forms of geometry, and most of these could probably be used by the theory we are now discussing, we will limit our article to the sort of geometry usually referred to as Euclidean Geometry. The primary reason for doing so is that the everyday world is a Euclidean space (e.g., parallel lines never cross, the corners of triangles have a total of 180 deg, and so on). To be most directly useful in dealing with common relationships a perceptual theory must predict how Euclidean relationships fit together. Basing a theory on a “non-Euclidean” form of mathematics would require that we include a transformation at some point to go back-and-forth. Occam’s razor states that we would do better if we adopt the simplest approach.

That said, Table 1 provides a list of the three Primary Variables and a list of several Derived Variables. Note that horizontal lines across the table do not have any direct correspondence. A given Derived Variable may be manipulated by changes in one, two or all three Primary Variables, as long as the laws of geometry are followed.

Table 1    The three Primary Variables of the Theory of Phenomenal Geometry and some of the perceptual
                 variables that may be derived from them, by applying the laws of Euclidean Geometry.

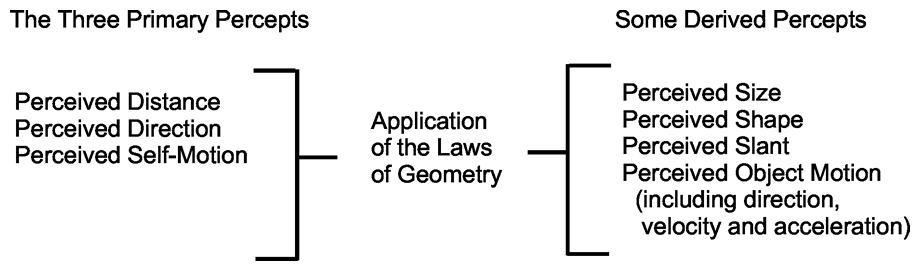
In considering this theory, it is crucial to recognize that every variable (regardless of its column in Table 1) is a perceptual one. Although we will consider some more limited, hybrid models in later articles, there are no physical variables specified in Table 1 – hence, the description as a Theory of Phenomenal Geometry. It is a model in which different percepts can be related to one another in predictable ways.

The Primary Variables

Perceived Distance refers to how far away an object appears from oneself (or from a specific observer). Perceived distances and perceived relative distances (depth) depend, as described earlier, upon a collection of cues, weighting principles and built-in tendencies. Although these obviously include some physical factors, it is the resulting perceptual value that is the primary variable.

Perceived Direction refers to the apparent direction between the observer and a point on a target object. In simple terms, would one point up or down, left or right, frontwards or to the back? By what angle, relative to one’s own position? For clarity, assume that one first observes a particular visual target itself, but then points after all the lights have been extinguished. That is, the act of pointing is an attempt to indicate one’s perception of direction, not the task of aligning a visible fingertip with a simultaneously visible object.

Some of the physical variables that can contribute to perceived direction (for a visual object) include the location of the object’s image on the retina, the orientation of the eye in the head, the orientation of the head (and body). However, one must also include…….(classes of illusion that may influence apparent direction).

Perceived Self-Motion refers to how, in what direction and at what velocity and acceleration, one perceives oneself to be in motion. (Note that it would be equally important, if one felt oneself to be completely stationary – that is, not moving at all.)

Some of the variables that often affect the perception of self-motion include inputs from the vestibular system (parts of the inner ear that include the semi-circular canals), whether properly registering changes in the body relative to the outside world or responding to orientational illusions, such as the inversion illusion in which the observer feels him/herself to be upside down from what is the case in reality. Other inputs that affect one’s sense of self-motion include the cutaneous and kinesthetic body senses.

And, in one of the few crossover factors relevant to Phenomenal Geometry, self-motion is well known to be affected by certain kinds of visual stimulation. Recall the effects when one is stopped in a car at a traffic light or sitting physically motionless in a train at the station. If another car pulls up beside your own, or a train rushes by on an adjacent track, you may have had the very strong impression that you yourself have begun to move. In years past, amusement parks often featured a ride called Cleopatra’s Barge. Riders sat in what seemed a large open boat, enclosed in a large darkened shed. After a pitchman’s build-up, the ceiling above the barge (painted with stars) began to roll back-and-forth in ever increasing arcs. Sitting below this sky, one felt oneself to be swinging back-and-forth under a stationary sky. Following several increasingly large swinging movements, the “sky” was rolled entirely over – to the screams of the riders who felt themselves suddenly being turned upside down.

The astute reader will note that, up to this point, the described primary variables are mostly tied to different types of external input or stimulation. (The two main exceptions are, of course, the optical illusions that influence the sense of self-motion and the two special autochthonous tendencies for depth and distance.)

Derived (or Secondary) Variables

Perceived size refers to how large or small an object appears. Perceived shape and slant are similarly related to how an object appears. Perceived object motion refers to how perceptual objects appear to move. (It is critical to remember that there is a significant difference between perceived self-motion and perceived object motion.)

The Theory of Phenomenal Geometry serves two purposes

First. The Theory can be considered as a description of how our perceptual systems combine external information to provide the wide variety of experiences involving the world around ourselves. That is, some external information is used to create a few internal variables that are the Primary Percepts. The Theory continues by arguing that these primary percepts will be combined in a manner consistent with geometrical laws, to form the characteristics we call the Derived Percepts. (Note that this is not equivalent to a statement that the brain is in any way aware that it is following predictions from Euclid; the outcomes are simply consistent with Euclidean geometry.)

Second. The Theory provides researchers (and/or other interested individuals) a basis for predicting how people are most likely to see their world. For instance, if one knows an observer's perceptions of distance, direction and/or self-motion, one can make more informed predictions about how large an object may appear or how it may seem to move. (In practice, accurate measurement of perceptual qualities, even the primary variables, is not easy. Nevertheless, the more one knows about the primary factors, the better one should be at predicting other aspects of the observer's perceived environment.

Final Note

Additional articles will provide examples of how phenomenal geometry works. Aside from recalling which variables are primary and which are derived, the most crucial thing to remember is that ALL variables in a true phenomenal geometry are perceived values. Although some of the later examples (in other articles) will involve a hybrid model that allows – for the sake of simplicity – one physical factor, it is important to recall that such variations are not fully phenomenal and that such models are always hybrids.

Those who wish to read about the Theory of Phenomenal Geometry in greater depth can read relevant Advanced Articles at this web site, or can attempt Gogel's original paper. That paper is: Gogel, W.C. (1990). A theory of phenomenal geometry and its applications. Perception & Psychophysics, 48, 105-123.